magic & skateparks: a pseudo-physical analogy
You and your opponent lock eyes over the crest of the boulder. You dig in your heels, brace your hands. When the ref shouts "go!", adrenaline and oxygenated blood race through you. You and your opponent are standing in a skatepark "bowl" -- a depression with shallow sloping sides -- each trying to push the boulder to the rim of the opponent's side, like a
tug-of-war shove-of-war. You're keenly aware of how the environment affects this contest of strength -- your traction on the ground, the size of the boulder, the endurance of both contestants, the steepness of the bowl.
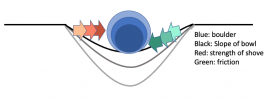
Such a game actually exists: it's called
Magic: The Gathering, and I've just described its physics.
Physics -- the science of understanding how and why the world behaves as it does -- maps surprisingly well onto game design. Indeed, many a game designer's commonest jargon are directly borrowed from physics. To wit: Games can be conceived as an "idealized system" governed by "mechanics" and described by a "game state". These are
all physical terms. Physicists study the behavior of subsets of reality (idealized systems) governed by absolute rules (mechanics) and described using metrics (a state). Analogies between the two disciplines are useful because humans have direct sensory experience with physics, which can help explain why and how game phenomena occur.
Let's apply the skatepark to a Magic game. Before the coin is flipped for first player, the game state is that of perfect equilibrium (the boulder at rest at the bowl's lowest point). The goal of each player is to reach a final state of victory (the boulder pushed up the bowl to the opponent's side). And so they enact game actions to pursue that goal (shoves on the boulder). But it's not merely a contest of brute strength; there are also environmental factors to consider...
For one, a bigger boulder will be harder to shove. This is a Magic format's
speed, which the designer can change directly by changing the starting life totals or other resources (commanders, conspiracies, fast mana, etc). It's also possible to alter a format's speed by lowering the mana curve, or changing the "clock" presented by the format's threats (
Terrain Elemental instead of
Grizzly Bears).
Second, not every shove is of equal strength. This is a Magic card's
rate.
Tarmogoyf is better than
Grizzly Bears at pushing the game to a conclusion. When a bunch of individual rates are bundled into a format, we call that
power level. Note the analogy's limits: a more powerful card will often win faster, too, which affects the format's perceived speed. I'm not trying to create an airtight analogy, merely illustrate the key differences between these ideas.
Third, the downward-sloping sides of the skatepark bowl mean shoves must be sustained over time -- the more sloped, the more sustained effort it takes to win. When Magic cards have a continuing effect on the game, we call this
snowballing (or the lack thereof). For example,
Dragon's Rage Channeler is slow to get going but can continue to provide value and evasive damage even in the late game;
Wild Nacatl scales to 3/3 more easily but can't scale through evasion. A deck composed of Wild Nacatls will struggle to win late games compared to a deck full of DRC, and both will struggle against
Pteramander, who scales slowest of all three but has the highest ceiling. For the
Wild Nacatl player to win games, they need to overwhelm the opponent quickly. The interplay of quick and slow scaling creates the
tempo dimension of a Cube, like the sloping sides of the skatepark bowl determine the difficulty of winning the game (and no, I'm not defining that word any more rigorously than this).
Finally, even the most well-placed boulder shove, intended to convert energy into motion, is not 100% efficient: friction causes energy to dissipate into the surroundings, unrecoverable. Magic cards are intended to convert resources (cards, mana, life, turns) into victory, but there are still losses. When a card like
Lion Sash is purchased for


, some fraction of that pays for the grave-hate utility of the Sash, and another pays for the Reconfigure utility. If those affordances aren't useful in a given game state, then part of the payment was wasted!
Efficient card designs recover this lost energy --
Goblin Guide recovers its drawback wastage by ending the game before the extra lands are relevant;
Murktide Regent recovers the wasted turns spent playing
cantrips by growing so big and cheap as to win the game by itself. Efficient formats (or, less ambiguously, formats with low
dissipation) are full of these kinds of cards.
| Skatepark Shove-of-War | A Magic Card | A Magic Format | Classical Physics (for the nerds) |
|---|
| The strength of a shove | Rate (per mana spent) | Format power level | Force |
| The slope of the bowl | Ability to scale into the late game | Format tempo | Resistance/springiness |
| The traction on the ground | "Friction": the efficiency of converting resources into useful, synergistic power | Format dissipation | Dissipation/friction |
| The size of the boulder | The speed of a card (its castability & clock) | Format speed | Mass, the resistance of an object to the effects of force (see 1) |


Anthony of
Lucky Paper makes the compelling case that power is relative in Limited -- a card like
Behold the Unspeakable may be worse in Modern than
Murktide Regent, but it's possible to design a cube where Behold is
relatively as strong as Murktide is in Modern. I think this is correct, but this begs the question -- will a Murktide cube have the same
play pattern as a Behold cube? And, whether or not this is true,
why?
Let's try a thought experiment: is it possible to vary the card design axes of rate, scalability, and dissipation independently? I'll provide two examples for each combination of these axes:
Small Rate (Behold Cube)
High Rate (Murktide Cube)
I suspect the answer lies in the way my skatepark analogy breaks. Push the boulder as hard as you like: do you expect to see the friction of the ground change as a result? what about the slope of the bowl? Of course not! These physical phenomena are
independent.
But I don't think that's the case in Magic design, because we're working with a finite card pool. Rate, speed, dissipation, and scalability are convoluted -- R&D only has a limited ability to turn one knob without bumping the others. In other words, it may be possible to make
Behold as relatively
strong as
Murktide, but it's unlikely that Behold will be as
snowballing, low-dissipation, and
fast as Murktide.


Those who've read my blog before know that
my fondest wish is for
Glissa, the Traitor to see play in my Cube. I love the deckbuild decisions she inspires, and I love how her ability (which can get value within the same turn cycle) makes her modal between "baneslayer" and "mulldrifter" depending dynamically on the game state.
But Glissa is... not good in The Ship of Theseus. Even more accurate: I've literally never seen her contribute to anything resembling a winning play pattern. At first, I thought she was simply too weak, so I kept
cutting, and
cutting, the format's power outliers. Eventually Glissa was plausibly the strongest BG threat at 3 MV,
Mob Nixilis was the strongest BR threat,
Slogurk was the strongest UG... And the format kept rejecting these threats, like an immune system rejects an intruder.
Contrast Glissa with
Mathas, Fiend Seeker. They both have 3/3 bodies, difficult costs, relevant keywords, and card-advantage engines that require other game pieces to reach their ceilings. The key difference is in the designs' dissipation of investment. A big fraction of Glissa's mana is "wasted energy" if you don't have 1) an artifact, 2) a way to put the artifact in your
grave, 3) several turns with Glissa in play, and at least one of 4) a kill spell or 5) combat phases. Mathas dissipates very little mana -- his Bounty persists even if he eats a kill spell, his trigger has an extremely narrow window of interaction, and can be triggered by
any card type. Sure, Mathas can't kill things by himself, but what experienced opponent ever blocks Glissa, anyways? Mathas is
vastly more successful in The Ship of Theseus than Glissa, even though they've both had stints as the highest-rate threat in their respective slots.
Patrick Sullivan, when
defining "efficiency" in the sense I use it, notes that efficient designs close off angles of attack for the opponent: you can't out-card
Uro, you can't out-race it, you can't out-tempo it. Moreover, efficient cards tend to linearize and streamline deckbuilding -- instead of compensating for your cards' weaknesses, you just go all-in on Plan A. Some amount of this is good in a Cube, but The Ship of Theseus is chock-full of
cards like this.
Even the non-creature spells are super-efficient -- instead of dissipating mana on things like
dynamic upside or
modality, they all do
exactly one thing, at a brutal rate. (These spells are consistutive for high-power Magic, but they function as the "white blood cells" that reject dissipative threats.)
My experiments in altering the power level of my format to showcase dissipative threats were thwarted by the way my metagame rewards frictionless cards and gameplans. I kept trying to insert
dissipative threats into an
efficient format.
TL;DR
1 - just because a threat is best-in-class, doesn't mean it will see play
2 - a format's dissipation sets the opportunity cost and rules of engagement for synergistic play patterns
3 - a frictionless format will reject dissipative cards (e.g. NEO's rejection of Samurai "Exalted"), often via the efficiency of the format's bread-and-butter effects
4 - because higher-power card designs are usually faster, more efficient, and more snowbally, it's not always possible to integrate dissipative threats (ie, threats that require synergy) into high-power formats


