General Fight Club
- Thread starter Jason Waddell
- Start date
regrowth costs less so an easy win for me. but if you’re doing some dedicated self mill and decks aren’t able to pressure you out of the game, revival gives you more value.
I'm currently testing Revival over Regrowth. Self-mill is a significant theme in my green section and I cut pretty much all of my non-creature spell velocity suite.
I am a bit worried about how slow it is, but it's interesting enough to test. I have enough experience with Regrowth at this point.
I appreciate the long-form response. I think your arguments are better in context. Most of what you are saying is largely correct, but there are a couple of points that I wish to respond to.
In context, I see the point you are arguing against is playing 70, 80, or 90 lands at 36o Cube size. That amount of fixing isn't even close to necessary for smaller, slower Cubes, especially at low power levels. I also understand that Blacksmithy really likes pushing high amounts of fixing in that range. However, the first posts in this thread are just someone saying "you run more fixing than the rest of us," and then someone replying with "try [playing more fixing], you'll like it," which doesn't actually tell the reader the extent that "more fixing" means. When arguing against that position, it can really sound like you're arguing against fixing in general, which is not what you meant but definitely what it comes off as saying.
I made my first post because as a content creator, I think it's important to advocate for design theory that is going to apply to a plurality of Cube designers. This forum is an extremely public space, where hundreds of people outside of the relatively small number of active members visit every day to read design theory. One thing I consistently notice with newer designers is that they will often skimp on lands against the best interest of their format. So when a post is made that lacks context as a counterpoint to something which is generally speaking good advice, I see that as something which could potentially be doing harm.
I'm not saying that every Cube would be improved by playing between 70 and 80 lands with snow duals in the basic land box, but saying that it would make the drafting and playing experience a lot worse as a blanket statement is just flat out wrong. There are clear and high-profile examples proving the opposite is true.
Heres's a helpful chart I made to help people visualize what I am saying:
Assuming a Cube has a base mono-color section of 50 cards per color and is playing 4 fixing lands per two-color pair, we can calculate the exact relationship between the percentage of playable spells removed from a section compared to the percentage of playable fixing added to a section. If we remove 2 spells per color to add 1 fixing land to a two-color pair, we remove 4% of the spells from a section, but we add 20% more fixing. 4% of a limited pool isn't all that noticeable, especially considering that only 23 to 25 spells are going to be played in the average deck, while most two-color decks will play every single nonbasic land they can get their hands on. A drafter will notice the sizable increase in fixing they are able to play, they won't notice the relatively small number of spells missing to give them that fixing.
There are diminishing returns with adding additional lands, as the %increase in fixing for every two cards removed goes down. However, the point at which the total percentage of spells removed to play more fixing goes above the percentage fixing increase is actually much higher than you would think. Assuming the same 50 cards per color and is playing 4 fixing lands per two-color pair split as before, the point at which adding more lands is less impactful than retaining more spells is 8 lands per two-color pair. Going from 7 to 8 lands is only a 12% increase in fixing, while 16% of spells per color are removed.
In short, when we're dealing with small numbers such as fixing lands per pair compared to large numbers such as spells per monocolor section, the material benefits gained from adding to the small section outweighs the losses from another section until we are basically doubling the small section. I'm not saying that every Cube should be adding lands until they reach the point of dimishing returns, not every Cube needs that level of fixing to function. I am saying that removing spells from a mono color section is going to be felt less by drafters than the increase in fixing they are going to be reciving as a result of that exchange. And again, this is all assuming these cuts are being made from mono-color sections and not elsewhere in the Cube.
This isn't my main point (which is a shame because it takes up a ton of space on the post), but I just wanted to point out that what you are saying is missing the broader mathematical exchange going on here.
Conclusion
It is really hard to build a Cube with too much fixing because making room for a huge density of lands is difficult, it is really easy to build a Cube with not enough fixing because cutting lands for spells is extremely tempting. I think it is irresponsible to advocate against the general idea of "more fixing" in a highly public setting given the propensity of new designers to skip on fixing. Most Cube designers could safely run more fixing and only have a positive impact on their format. The average Cube likely won't need the density of lands that Blacksmithy likes to use, but there are lots of Cubes that need that density. It's fine to advocate against playing 70-80-90 lands as a general concept for "normal" Cubes, but that needs to be clear to the reader. Otherwise, people might assume you're saying fixing is bad and they should be playing less. You need to be really careful to provide enough context when making general statements because you could end up leading people in a direction contrary to your own personal position.
In context, I see the point you are arguing against is playing 70, 80, or 90 lands at 36o Cube size. That amount of fixing isn't even close to necessary for smaller, slower Cubes, especially at low power levels. I also understand that Blacksmithy really likes pushing high amounts of fixing in that range. However, the first posts in this thread are just someone saying "you run more fixing than the rest of us," and then someone replying with "try [playing more fixing], you'll like it," which doesn't actually tell the reader the extent that "more fixing" means. When arguing against that position, it can really sound like you're arguing against fixing in general, which is not what you meant but definitely what it comes off as saying.
I made my first post because as a content creator, I think it's important to advocate for design theory that is going to apply to a plurality of Cube designers. This forum is an extremely public space, where hundreds of people outside of the relatively small number of active members visit every day to read design theory. One thing I consistently notice with newer designers is that they will often skimp on lands against the best interest of their format. So when a post is made that lacks context as a counterpoint to something which is generally speaking good advice, I see that as something which could potentially be doing harm.
I dislike this argument because it implies that there is no Cube that is correctly running more than a certain amount of fixing, which is categorically untrue. You don't even have to go far to find Cubes running fixing in roughly the same ratio as your argument. For example, @landofMordor's Cube has roughly 74 fixing lands per 360 cards. My friend Lyra has a Cube with roughly 70 lands per 360 cards and also has Kaldheim snow duals in the basic land box. Both of these Cubes are fun to play and are better because they have I get that your argument here is a sort of strawman meant to showcase the "absurdity" of running a land density for hyper-consistent fixing. However, it misses the fact that there are Cubes that need fixing of this quantity in order to function correctly, and are actively improved by having these fixing ratios.
I'm not saying that every Cube would be improved by playing between 70 and 80 lands with snow duals in the basic land box, but saying that it would make the drafting and playing experience a lot worse as a blanket statement is just flat out wrong. There are clear and high-profile examples proving the opposite is true.
But there's also something that you're not considering: the relationship between the percentage increase of playable fixing in relation to the decrease in playable spells.
Heres's a helpful chart I made to help people visualize what I am saying:
Assuming a Cube has a base mono-color section of 50 cards per color and is playing 4 fixing lands per two-color pair, we can calculate the exact relationship between the percentage of playable spells removed from a section compared to the percentage of playable fixing added to a section. If we remove 2 spells per color to add 1 fixing land to a two-color pair, we remove 4% of the spells from a section, but we add 20% more fixing. 4% of a limited pool isn't all that noticeable, especially considering that only 23 to 25 spells are going to be played in the average deck, while most two-color decks will play every single nonbasic land they can get their hands on. A drafter will notice the sizable increase in fixing they are able to play, they won't notice the relatively small number of spells missing to give them that fixing.
There are diminishing returns with adding additional lands, as the %increase in fixing for every two cards removed goes down. However, the point at which the total percentage of spells removed to play more fixing goes above the percentage fixing increase is actually much higher than you would think. Assuming the same 50 cards per color and is playing 4 fixing lands per two-color pair split as before, the point at which adding more lands is less impactful than retaining more spells is 8 lands per two-color pair. Going from 7 to 8 lands is only a 12% increase in fixing, while 16% of spells per color are removed.
In short, when we're dealing with small numbers such as fixing lands per pair compared to large numbers such as spells per monocolor section, the material benefits gained from adding to the small section outweighs the losses from another section until we are basically doubling the small section. I'm not saying that every Cube should be adding lands until they reach the point of dimishing returns, not every Cube needs that level of fixing to function. I am saying that removing spells from a mono color section is going to be felt less by drafters than the increase in fixing they are going to be reciving as a result of that exchange. And again, this is all assuming these cuts are being made from mono-color sections and not elsewhere in the Cube.
This isn't my main point (which is a shame because it takes up a ton of space on the post), but I just wanted to point out that what you are saying is missing the broader mathematical exchange going on here.
Conclusion
It is really hard to build a Cube with too much fixing because making room for a huge density of lands is difficult, it is really easy to build a Cube with not enough fixing because cutting lands for spells is extremely tempting. I think it is irresponsible to advocate against the general idea of "more fixing" in a highly public setting given the propensity of new designers to skip on fixing. Most Cube designers could safely run more fixing and only have a positive impact on their format. The average Cube likely won't need the density of lands that Blacksmithy likes to use, but there are lots of Cubes that need that density. It's fine to advocate against playing 70-80-90 lands as a general concept for "normal" Cubes, but that needs to be clear to the reader. Otherwise, people might assume you're saying fixing is bad and they should be playing less. You need to be really careful to provide enough context when making general statements because you could end up leading people in a direction contrary to your own personal position.
Speaking as someone who has recently jumped from 30 to 60 fixing lands, I can report that it's definitely made a huge difference in how my (solo, bot-enabled) drafts have gone. I'm not sure it's been entirely for the better, and my data is definitely skewed by how the CubeCobra bots will gobble up fixing like no one other than my friend Emmett, but the mana definitely feels easier to make work. However, I definitely feel the pinch in terms of my slots for each color.
I will say, the biggest jump for me lay in adding the fetches. My original base was pathways, bounce lands, and a split cycle of horizons and bicycles, so to add fetches meaningfully meant that I had to add in fetchable lands like the tangos and triomes, and I balanced them out with the fast lands to throw a bone to decks that hate tapped lands.
The biggest downside to this jump in lands was that they all seemed to blur together. I've found myself no longer considering the specific advantages and disadvantages of Cinder Glade as opposed to Copperline Gorge and simply scooped it up. Maybe this means that I should simplify the manabase to have 2 cycles of fetches, 2 cycles of completed bicycle lands, and 2 cycles of completed horizon lands, but that feels weird too. It's probably just an issue with adjusting to the new cube format, tbh.
Anyways, that's my experience so far. We'll see where I wind up, but it's been a fun experiment trying to port my favorite set of archetypes into a radically different environment without massively spiking the power level and thereby losing my "personal cube staples."
I will say, the biggest jump for me lay in adding the fetches. My original base was pathways, bounce lands, and a split cycle of horizons and bicycles, so to add fetches meaningfully meant that I had to add in fetchable lands like the tangos and triomes, and I balanced them out with the fast lands to throw a bone to decks that hate tapped lands.
The biggest downside to this jump in lands was that they all seemed to blur together. I've found myself no longer considering the specific advantages and disadvantages of Cinder Glade as opposed to Copperline Gorge and simply scooped it up. Maybe this means that I should simplify the manabase to have 2 cycles of fetches, 2 cycles of completed bicycle lands, and 2 cycles of completed horizon lands, but that feels weird too. It's probably just an issue with adjusting to the new cube format, tbh.
Anyways, that's my experience so far. We'll see where I wind up, but it's been a fun experiment trying to port my favorite set of archetypes into a radically different environment without massively spiking the power level and thereby losing my "personal cube staples."
Nice analysis, but the individual card loss/gain amount and the actual requirements of drafting decks in a format should be weighed in too.
Removing two cards per color removes 4 cards from a color pair. Adding one cycle of fixing adds 1 card per pair. You are losing 4x as many nonlands per swap compared to gains in lands; overall decrease of 3 cards per swap. Often these swaps come from more niche and/or slightly less played options, so a format can lose granularity a lot more quickly than one might expect. This means that we should be looking for a balance where the needs of the format's decks are being met while preserving as much of that granularity as possible.
(basically, nonlands do more interesting things than lands, we should try to preserve as many nonlands as possible)
Depending on the desired color count of the average deck in a format:
If the format's decks want 1.5 to 2 colors (retail oriented perhaps), you have [number of lands in a pair] available fixing lands for each drafter, and depending on format speed a varying requirement for lands in a final deck. Even 1 or 2 fixing lands is sufficient in many cases (see below). At 5 or more duals deck performance is virtually indistinguishable except at very high game counts because 5 lands is already >95% efficacy (also see below).
If the format-average deck is 2.5 to 3 color, you have 3x [number of lands in a pair] available to each drafter. There will be competition of course, but even at 4 cycles, every drafter has the potential to see 12 relevant fixing lands. By the time there are 6 land cycles, each drafter can see 18 relevant lands in the draft, more than a draft deck will even use normally. At 8 cycles you have 24 relevant lands available per deck in a draft. In either of the latter two cases I argue below that that is already more than sufficient.
Based on the suppositions above, I argue that 5 fixing cycles is sufficient and potentially ideal for many formats (mine included). Note that all 400 of my cards show up in most of my drafts.
Above cycle count 5 what is happening is reduction in the opportunity cost of lands, not necessarily an increase in the ability of decks to draft the mana they need. And that reduction of opportunity cost is coming with a correspondingly larger reduction in per-pair options. Going from 4 to 8 cycles removes 12 options from a color pair. That is an impactful reduction for the drafter and cube designer. Checking that reduction using the original numbers from above and adding in some artifacts and multicolored spells: With the original four cycles we have (50 color A + 50 color B + 4 Land + 3 Multi + 40 artifact = 147 available). Upping to 8 cycles we have (42 color A + 42 color B + 8 Land + 3 Multi + 40 artifact = 135 available). that is a 8.5% decrease in total options for a color pair. That percentage gets higher if some of the cards aren't relevant to that particular build, which is typically true. With some realistic restrictions on relevant cards we hit 10+% reduction in choices fairly quickly (removal of just 25 options due to irrelevance gets us there).
Important to note that 3+ color decks are not affected equally. 3 color decks only see a 5.7% reduction in choices. 4 color decks see <3% drop in choices. Both have much larger pools of cards to draw from.
So what you end up with is a skewed reduction in cards available to different decks, combined with less effort needed to grab more lands for higher color counts (beyond what is technically needed). That can lead to 2 color decks becoming less competitively viable as the relatively lower loss of choices at 3+ colors becomes more palatable due to low land opportunity cost. That reduction in viability can become a reduction in format variability (31 -> 16 viable color combinations assuming total invalidation of 1 and 2 color decks, which isn't likely, but is illustrative). This besides the fact that reducing monocolor sections often comes at the expense of more niche or fragile buildarounds that aren't vital to the formats goals.
TL;DR: fixing % does increase very rapidly as cycles are added. But available cards per pair decreases as lands are added so we should try to find a balance. Fixing efficacy caps out relatively quickly, and also quickly becomes a meaningful reduction in available choices. That can mean reduction in viable archetype "flavors" drafted. The conclusion I've arrived at and used in my formats is that 5 cycles is the optimum, but see 6 cycles working well too.
Removing two cards per color removes 4 cards from a color pair. Adding one cycle of fixing adds 1 card per pair. You are losing 4x as many nonlands per swap compared to gains in lands; overall decrease of 3 cards per swap. Often these swaps come from more niche and/or slightly less played options, so a format can lose granularity a lot more quickly than one might expect. This means that we should be looking for a balance where the needs of the format's decks are being met while preserving as much of that granularity as possible.
(basically, nonlands do more interesting things than lands, we should try to preserve as many nonlands as possible)
Depending on the desired color count of the average deck in a format:
If the format's decks want 1.5 to 2 colors (retail oriented perhaps), you have [number of lands in a pair] available fixing lands for each drafter, and depending on format speed a varying requirement for lands in a final deck. Even 1 or 2 fixing lands is sufficient in many cases (see below). At 5 or more duals deck performance is virtually indistinguishable except at very high game counts because 5 lands is already >95% efficacy (also see below).
If the format-average deck is 2.5 to 3 color, you have 3x [number of lands in a pair] available to each drafter. There will be competition of course, but even at 4 cycles, every drafter has the potential to see 12 relevant fixing lands. By the time there are 6 land cycles, each drafter can see 18 relevant lands in the draft, more than a draft deck will even use normally. At 8 cycles you have 24 relevant lands available per deck in a draft. In either of the latter two cases I argue below that that is already more than sufficient.
Based on the suppositions above, I argue that 5 fixing cycles is sufficient and potentially ideal for many formats (mine included). Note that all 400 of my cards show up in most of my drafts.
- First: as a point of reference for the capture rates mentioned below, the pairs experience the following "drafter need" listed out by average color count seen in decks in a given format:
1.5 color format: 0.4 drafters per color pair
2 color format: 0.8 drafters per color pair
2.5 color format: 1.6 drafter per color pair
3 color format: 2.4 drafters per color pair
4 color format: 4.8 drafters per color pair
First and a half: 90% is a very commonly thrown around number as the threshold to a constructed level of reliability. Kartsen etc. use this number, so it is the number I focus on too.
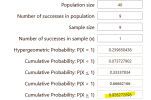
-Second: 5 fixing lands is sufficient for a 2 color deck in most circumstances. A deck with 5 duals will have a 96% chance of drawing a needed color by turn 2 (on theplaydraw). Even at only 1 successfully drafted out of 5 (20% capture rate) your chance for color happy times is still over 90% (analysis in second picture below). In a two color format that is drafted by reasonably experienced drafters guild representation should be relatively evenly spread. Even with 2 people directly competing in the same guild each can expect to snatch 2.5 fixing lands, which provides >90% efficacy.
Two color deck capturing 100% of relevant lands:
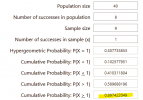
-Third: 15 lands is more than sufficient for the average three color deck. Even with only 60% of that available pool successfully drafted, you have an over 90% chance to draw the land you need by turn 2, and even with only 40% successfully captured, you are still hovering right at 90% success rate. This is assuming a decently even distribution of colors inside a deck, which isn't always the case. the math gets trickier with a splash color, but lower land counts are tenable in such a 2.5 color deck. With 2.4 drafters competing for given fixing real estate, one can expect approximately a 42% capture rate on average, which is shown to be workable.
Three color deck capturing 60% of relevant lands, or 2 color deck capturing 20% of available lands:
Three color deck capturing 40% of relevant lands:
1.5 color format: 0.4 drafters per color pair
2 color format: 0.8 drafters per color pair
2.5 color format: 1.6 drafter per color pair
3 color format: 2.4 drafters per color pair
4 color format: 4.8 drafters per color pair
First and a half: 90% is a very commonly thrown around number as the threshold to a constructed level of reliability. Kartsen etc. use this number, so it is the number I focus on too.
-Second: 5 fixing lands is sufficient for a 2 color deck in most circumstances. A deck with 5 duals will have a 96% chance of drawing a needed color by turn 2 (on the
Two color deck capturing 100% of relevant lands:
-Third: 15 lands is more than sufficient for the average three color deck. Even with only 60% of that available pool successfully drafted, you have an over 90% chance to draw the land you need by turn 2, and even with only 40% successfully captured, you are still hovering right at 90% success rate. This is assuming a decently even distribution of colors inside a deck, which isn't always the case. the math gets trickier with a splash color, but lower land counts are tenable in such a 2.5 color deck. With 2.4 drafters competing for given fixing real estate, one can expect approximately a 42% capture rate on average, which is shown to be workable.
Three color deck capturing 60% of relevant lands, or 2 color deck capturing 20% of available lands:
Three color deck capturing 40% of relevant lands:
Above cycle count 5 what is happening is reduction in the opportunity cost of lands, not necessarily an increase in the ability of decks to draft the mana they need. And that reduction of opportunity cost is coming with a correspondingly larger reduction in per-pair options. Going from 4 to 8 cycles removes 12 options from a color pair. That is an impactful reduction for the drafter and cube designer. Checking that reduction using the original numbers from above and adding in some artifacts and multicolored spells: With the original four cycles we have (50 color A + 50 color B + 4 Land + 3 Multi + 40 artifact = 147 available). Upping to 8 cycles we have (42 color A + 42 color B + 8 Land + 3 Multi + 40 artifact = 135 available). that is a 8.5% decrease in total options for a color pair. That percentage gets higher if some of the cards aren't relevant to that particular build, which is typically true. With some realistic restrictions on relevant cards we hit 10+% reduction in choices fairly quickly (removal of just 25 options due to irrelevance gets us there).
Important to note that 3+ color decks are not affected equally. 3 color decks only see a 5.7% reduction in choices. 4 color decks see <3% drop in choices. Both have much larger pools of cards to draw from.
So what you end up with is a skewed reduction in cards available to different decks, combined with less effort needed to grab more lands for higher color counts (beyond what is technically needed). That can lead to 2 color decks becoming less competitively viable as the relatively lower loss of choices at 3+ colors becomes more palatable due to low land opportunity cost. That reduction in viability can become a reduction in format variability (31 -> 16 viable color combinations assuming total invalidation of 1 and 2 color decks, which isn't likely, but is illustrative). This besides the fact that reducing monocolor sections often comes at the expense of more niche or fragile buildarounds that aren't vital to the formats goals.
TL;DR: fixing % does increase very rapidly as cycles are added. But available cards per pair decreases as lands are added so we should try to find a balance. Fixing efficacy caps out relatively quickly, and also quickly becomes a meaningful reduction in available choices. That can mean reduction in viable archetype "flavors" drafted. The conclusion I've arrived at and used in my formats is that 5 cycles is the optimum, but see 6 cycles working well too.
Last edited:
just want point out that all of this is correct, and it’s a reason i wanted to do what i do, as i see encouraging 3+ color decks and cutting fragile buildarounds as good things to be doing to a format
That's very fine and good and cool if it's directly benefitting the format you are aiming for. I'm just highlighting that increased land count doesn't equal unilaterally better things for a format, it yields concrete shifts in how drafts and decks happen. And those shifts may very well be counter to the health of the desired format. For instance, anyone who actively wants to field monocolor archetypes would do very well to shy away from excess lands.
(And of course some of the discussion above is totally thrown out your particular window because you artificially increase the nonland options in a draft, removing many of the downsides mentioned in my post).
So, one thing I've noticed is that the "decks not cards" philosophy pushes you towards two conflicting extremes:
A) WotC-Style Limited Cube, where you have a bunch of overlapping "themes", with bombs inside those themes that help pull things together.
B) Constructed-Style Cube, where you have a number of "ideal" decks (with engines and payoffs) that people are building towards.
My (unsubstantiated) hunch is that the people who are advocating for plentiful fixing have lists that lean towards B. Like, you definitely can have an A-style cube with incredible fixing or a B-style cube with terrible fixing, but at first blush I'd say that B-style cubes are more likely to be color-hungry.
I dunno. I might be talking out of my ass here.
A) WotC-Style Limited Cube, where you have a bunch of overlapping "themes", with bombs inside those themes that help pull things together.
B) Constructed-Style Cube, where you have a number of "ideal" decks (with engines and payoffs) that people are building towards.
My (unsubstantiated) hunch is that the people who are advocating for plentiful fixing have lists that lean towards B. Like, you definitely can have an A-style cube with incredible fixing or a B-style cube with terrible fixing, but at first blush I'd say that B-style cubes are more likely to be color-hungry.
I dunno. I might be talking out of my ass here.
retail limited makes me rage and my cube makes me happy so i think my cube is type B, this tracks
I think that's roughly correct. I think it might have to do a little more with environment speed than simply "more like constructed" or "more like retail." A lightning-fast retail style format (like one mirroring triple Zendikar, for example), is probably going to want more fixing than a format mirroring a grindier format like, say, Hour of Devastation Hour of Devastation Amonkhet.
Good observation!
I think I agree with the general sentiment of this post, although there are a couple of details I disagree with. Granted, a lot of this discussion is kind of nebulous because there are so many different variables in Cube design. I don't think you're wrong, in any case, although I would like to scrutinize a couple of the details.
So it is true that once you start to get to 6 lands per pair, each drafter can see 18 relevant lands, which is often more than a single deck will use. However, when we're talking about three-color decks, it's worth remembering that a drafter will only get the "perfect" number if they are completely uncontested in the draft. Assuming we have a 2.5 color format here, that means roughly 4 players are going to be playing 3c decks, and 4 players are going to be playing 2c decks. That means, for every color pair, about 2 people on average are going to be looking to pick up lands for that pair. Since this hypothetical Cube only has 60 lands, that means that each player is only going to get 7.5 lands per deck, far from the 18 land theoretical yield. Assuming the 2-color drafters each get all of their correct lands, that means the average three color drafter is going to receive roughly 9 lands. That's still a decent number, but it is quite a bit lower than the maximum they could potentially get if they were drafting completely uncontested.
Even assuming perfect partitioning of resources, a player drafting a 3c deck at the same table as two players with overlapping colors is going to only going to get 12 lands. Again, a decent yield, but still not more than is necessary. The only point at which players will, on average, be drafting all of the lands they need to play in their deck is with 136 lands in the Cube. That's a little under double the "point of diminishing returns" I calculated in my previous post.
I don't know if 8% is a negligible difference, but I think in a Cube that wants 80 lands, those 12 or so spells that are missing probably wouldn't be missed. The only Cubes that really want 80+ lands are ones that are trying to enable fast, low to the ground 2-3 color decks. At that point, fixing is still a premium even with the reduced opportunity cost of land because you'll still need the tools to cast your spells effectively. It's just now, players don't have to worry about passing a Flooded Strand or something to take the Swords to Plowshares in the pack.
I think this is a reasonable conclusion for a lot of Cubes. 50 is probably the low end of where most 1.5-2.5 color formats want to be; I think 60 is likely a better baseline for Cubes trying to enable fast proactive 2-color decks. Right now I have 50 lands in my Cube, and I don't think that number is really where I want to be for 8 players. My average deck is supposed to be between 2 and 3 colors with the exceptions of Mono-Red and Mono-White, both of which are viable but have heavy overlap with Boros, Izzet, and Jeskai blitz/prowess decks. I've been drafting all 360 cards with 6 drafters, which has yielded fixing quantities roughly to my liking. However, that is not enough land for the same environment with 8 players. What that means is I likely need an extra 12-14 lands in order to ensure a mathematically similar density. I'm also considering adding the Bridges to my Cube's basic land box as a means to support a potential Artifact Pile deck, but I'm not sure about that yet. Since your Cube appears to be quite a bit slower than mine, and your gold section is smaller, 50 seems like a great number for you.
The main point of my posts has been to counter some of the potential negative implications of Ravnic's initial post, which reads as anti-fixing in general. Most Cubes don't run the 50-65 lands per 360 cards that we've kind of come to as a decent number in this exchange, and I think we can all agree that it would not be good if a newer cuber came here to learn about Cube design and left with bad information, even if that wasn't the intention of the initial post.
Thank you for the interesting conversation, I really appreciate your input!
I covered this in my "details" in the parts about drafters per color pair.
Even with 2.4 drafters competing for one slot I showed a sufficient land density to hit Karsten efficacy at 5 cycles.
12 lands *is* more than necessary for most formats as I show in my details section (6 duals is sufficient for 3C decks in many formats, where color consistency really starts being important on T2).
I had the same fear that @sigh had. That by adding too many fixing lands I would water down the playable cards per color. So I came up with the following solution:
My draft boosters contents are no entirely randomized. Just like the Mystery Boosters I have slots for each color, lands, artifacts etc. The cards which are added to the slots are randomized of course.
This makes constructing packs for the draft a little more complicated but everyone in my group loved the idea.
My draft boosters contents are no entirely randomized. Just like the Mystery Boosters I have slots for each color, lands, artifacts etc. The cards which are added to the slots are randomized of course.
This makes constructing packs for the draft a little more complicated but everyone in my group loved the idea.
Onderzeeboot
Ecstatic Orb
Cool! I do the same! I am considering to up my cube size a bit so I can add a land slot as the 16th card in the pack, after someone suggested that idea a few posts back. I'ld have to analyze my cube in light of Train's and
Last edited:
My packs have 16 slots, too!Cool! I do the same! I am considering to up my cube size a bit so I can add a land slot as the 16th card in the pack, after someone suggested that idea a few posts back. I'ld have to analyze my cube in light of Train's and sith's posts to see if that is needed
Onderzeeboot
Ecstatic Orb
1. The second image with 20% capture rate for a two-color deck is missing, I think?
2. If a 60% capture rate for a three color deck equates 9 duals, shouldn't a 40% capture rate equal *6* drafted duals? That would almost assuredly sink the P(X >= 1) well below 90%. I'm going to do some follow-up calculations once I haul my lazy ass out of bed.
highly highly recommend this. just a small bump to the cube size to allow for draft pools to go to 48-50, makes a huge difference in terms of giving you that leeway to shower your drafters in fixing while still having functional mono sections. you can cast your spells on time AND have spells to cast! win-win!Cool! I do the same! I am considering to up my cube size a bit so I can add a land slot as the 16th card in the pack, after someone suggested that idea a few posts back. I'ld have to analyze my cube in light of Train's and sith's posts to see if that is needed
landofMordor
Administrator
Hey, congrats on your new lands. Just wanted to mention some testing results of mine in this regard:
> I've realized that nobody actually likes the tracking complexity of EDH manabases. Half your brainpower is simply doing the accounting labor of filterlands or w/e to see if you can actually sequence properly. The specific nuance of each card is not net-fun-added, and is actively hostile to newer players, who will grok all the UB lands as being identical (because after all, the art is practically identical!) and then make sequencing mistakes with their River of Tears.
> I think my newer players can meaningfully track about 4-5 unique types of land at any time, but more than that and they'll frequently leave win% on the table just due to accounting errors. And that number goes down if the lands behave differently on the battlefield, like filterlands or creaturelands. I think the complexity is much better when it's located as the land is entering (fastland, shockland, etc) and then the land is a functional true dual.
> By contrast, when I went to all duals and fetches (and one cycle of shocks because they're not proxied and I'm vain) this situation improved a TON. I think this is a really elegant, complexity-decreasing and friendliness-increasing option, personally, and I'd encourage you to try it.
> I'm also surprised to hear that more lands made you consider their differences less. In a sparse-fixing world, I'd be desperate for any fixing even if it was all disadvantages.
--------
And skimming over the rest of the thread, I've found that increasing total cube size and draft pool size is a great way to increase fixing quantity without reducing space in the cube for archetype glue, build-arounds, or other fun stuff. It doesn't add too much to the complexity budget if you break singleton on some number of cycles.
Onderzeeboot
Ecstatic Orb
Okay, here goes! I like to work with examples, because that's how my brain works, and because they give an idea of how averages translate to the real world.
TLDR; Hahaha... Ha... ha... Oh, do I really have to write a synopsis?! o_O Ok then...
Assumptions:
- Drafters try to find an open lane
- Four drafters end up with a 2 color deck, four drafters end up with a 3 color deck
- Drafters value lands roughly equally in a vacuum
- All duals fix for two colors only
- Duals always end up with a drafter in those colors
I'm going to visually an 8 person pod to see what colors people end up in:
- Seat 1: WU
- Seat 2: WBR
- Seat 3: GU
- Seat 4: RW
- Seat 5: UBG
- Seat 6: WUR
- Seat 7: BR
- Seat 8: GWB
Yeah, that looks plausible to my eyes. We've got three white drafters in a row in seats 8 through 2, but that happens sometimes, and each one can lean on a different unique guild (GW, WU, and WR respectively). I once had a draft where three consecutive players somehow all ended up in Grixis! So, let's see how the each guild shakes out in terms of number of drafters.
- WU: 2
- UB: 1
- BR: 2
- RG: 0
- GW: 1
- WB: 2
- UR: 1
- BG: 2
- RW: 3
- GU: 2
Here, each guild is, on average, drafted by 16/10 = 1.6 drafters. Exactly as sigh told us, but we do see that it's entirely plausible for a color pair to be ignored, or slightly overdrafted (apparently Boros is really deep in this cube, weird).
What does this mean for capture rate? Well, we can map that out!
- Seat 1: 1/2 of WU duals
- Seat 2: 1/2 of WB duals, 1/2 of BR duals, 1/3 of RW duals
- Seat 3: 1/2 of GU duals
- Seat 4: 1/3 of RW duals (oh boy!)
- Seat 5: 1/1 of UB duals, 1/2 of BG duals, 1/2 of GU duals
- Seat 6: 1/2 of WU duals, 1/1 of UR duals, 1/3 of RW duals
- Seat 7: 1/2 of BR duals
- Seat 8: 1/1 of GW duals, 1/2 of WB duals, 1/2 of BG duals
- Drafters try to find an open lane
- Four drafters end up with a 2 color deck, four drafters end up with a 3 color deck
- Drafters value lands roughly equally in a vacuum
- All duals fix for two colors only
- Duals always end up with a drafter in those colors
I'm going to visually an 8 person pod to see what colors people end up in:
- Seat 1: WU
- Seat 2: WBR
- Seat 3: GU
- Seat 4: RW
- Seat 5: UBG
- Seat 6: WUR
- Seat 7: BR
- Seat 8: GWB
Yeah, that looks plausible to my eyes. We've got three white drafters in a row in seats 8 through 2, but that happens sometimes, and each one can lean on a different unique guild (GW, WU, and WR respectively). I once had a draft where three consecutive players somehow all ended up in Grixis! So, let's see how the each guild shakes out in terms of number of drafters.
- WU: 2
- UB: 1
- BR: 2
- RG: 0
- GW: 1
- WB: 2
- UR: 1
- BG: 2
- RW: 3
- GU: 2
Here, each guild is, on average, drafted by 16/10 = 1.6 drafters. Exactly as sigh told us, but we do see that it's entirely plausible for a color pair to be ignored, or slightly overdrafted (apparently Boros is really deep in this cube, weird).
What does this mean for capture rate? Well, we can map that out!
- Seat 1: 1/2 of WU duals
- Seat 2: 1/2 of WB duals, 1/2 of BR duals, 1/3 of RW duals
- Seat 3: 1/2 of GU duals
- Seat 4: 1/3 of RW duals (oh boy!)
- Seat 5: 1/1 of UB duals, 1/2 of BG duals, 1/2 of GU duals
- Seat 6: 1/2 of WU duals, 1/1 of UR duals, 1/3 of RW duals
- Seat 7: 1/2 of BR duals
- Seat 8: 1/1 of GW duals, 1/2 of WB duals, 1/2 of BG duals
Assumptions:
- We assume a 360 cube, so all duals in the cube are in the draft pool
- All duals fix for two colors only
- Duals always end up with a drafter in those colors
- Duals are evenly distributed if possible
- Remainders are distributed to 3 color drafters first (for example, if two players compete for 5 duals, the 3 color drafter will get 3 of them, and the 2 color drafter will get 2)
- Remainders will be split into fractions if more than one player has equal 'claim' on the remainder (e.g. two 3 color drafters have to split one remaining dual)
In our example in part the first, we found that drafters typically end up with 1/1, 1/2, or 1/3 of the total number of duals in a given guild. Using these fractions, we can calculate the average number of captured lands per guild based on the total number of duals the cube runs per guild.
- 4 duals per guild: 1/1 =4; 1/2 = 2; 1/3 = 1.33
- 5 duals per guild: 1/1 =5; 1/2 = 2.5; 1/3 = 1.66
- 6 duals per guild: 1/1 =6; 1/2 = 3; 1/3 = 2
- 7 duals per guild: 1/1 =7; 1/2 = 3.5; 1/3 = 2.33
- 8 duals per guild: 1/1 =8; 1/2 = 4; 1/3 = 2.66
Using these numbers and our assumptions, we can map out the expected number of captured lands for our example draft pod in part the first.
Now we can do a simple summation for this draft pod to calculate the total number of captured duals, depending on the total number of duals in the cube.
I like numbers.
- We assume a 360 cube, so all duals in the cube are in the draft pool
- All duals fix for two colors only
- Duals always end up with a drafter in those colors
- Duals are evenly distributed if possible
- Remainders are distributed to 3 color drafters first (for example, if two players compete for 5 duals, the 3 color drafter will get 3 of them, and the 2 color drafter will get 2)
- Remainders will be split into fractions if more than one player has equal 'claim' on the remainder (e.g. two 3 color drafters have to split one remaining dual)
In our example in part the first, we found that drafters typically end up with 1/1, 1/2, or 1/3 of the total number of duals in a given guild. Using these fractions, we can calculate the average number of captured lands per guild based on the total number of duals the cube runs per guild.
- 4 duals per guild: 1/1 =4; 1/2 = 2; 1/3 = 1.33
- 5 duals per guild: 1/1 =5; 1/2 = 2.5; 1/3 = 1.66
- 6 duals per guild: 1/1 =6; 1/2 = 3; 1/3 = 2
- 7 duals per guild: 1/1 =7; 1/2 = 3.5; 1/3 = 2.33
- 8 duals per guild: 1/1 =8; 1/2 = 4; 1/3 = 2.66
Using these numbers and our assumptions, we can map out the expected number of captured lands for our example draft pod in part the first.
4 duals per guild | 5 duals per guild | 6 duals per guild | 7 duals per guild | 8 duals per guild | |
| Seat 1 (1/2 WU) | 2 WU | 2 WU | 3 WU | 3 WU | 4 WU |
| Seat 2 (1/2 WB, 1/2 BR, 1/3 RW) | 2 WB, 2 BR, 1.5 RW | 2.5 WB, 3 BR, 2 RW | 3 WB, 3 BR, 2 RW | 3.5 WB, 4 BR, 2.5 RW | 4 WB, 4 BR, 3 RW |
| Seat 3 (1/2 GU) | 2 GU | 2 GU | 3 GU | 3 GU | 4 GU |
| Seat 4 (1/3 RW) | 1 RW | 1 RW | 2 RW | 2 RW | 2 RW |
| Seat 5 (1/1 UB, 1/2 BG, 1/2 GU) | 4 UB, 2 BG, 2 GU | 5 UB, 2.5 BG, 3 GU | 6 UB, 3 BG, 3 GU | 7 UB, 3.5 BG, 4 GU | 8 UB, 4 BG, 4 GU |
| Seat 6 (1/2 WU, 1/1 UR, 1/3 RW) | 2 WU, 4 UR, 1.5 RW | 3 WU, 5 UR, 2 RW | 3 WU, 6 UR, 2 RW | 4 WU, 7 UR, 2.5 RW | 4 WU, 8 UR, 3 RW |
| Seat 7 (1/2 BR) | 2 BR | 2 BR | 3 BR | 3 BR | 4 BR |
| Seat 8 (1/1 GW, 1/2 WB, 1/2 BG) | 4 GW, 2 WB, 2 BG | 5 GW, 2.5 WB, 2.5 BG | 6 GW, 3 WB, 3 BG | 7 GW, 3.5 WB, 3.5 BG | 8 GW, 4 WB, 4 BG |
Now we can do a simple summation for this draft pod to calculate the total number of captured duals, depending on the total number of duals in the cube.
4 duals per guild | 5 duals per guild | 6 duals per guild | 7 duals per guild | 8 duals per guild | |
| Seat 1 (WU) | 2 | 2 | 3 | 3 | 4 |
| Seat 2 (WBR) | 5.5 | 7.5 | 8 | 10 | 11 |
| Seat 3 (GU) | 2 | 2 | 3 | 3 | 4 |
| Seat 4 (RW) | 1 | 1 | 2 | 2 | 2 |
| Seat 5 (UBG) | 8 | 10.5 | 12 | 14.5 | 16 |
| Seat 6 (WUR) | 7.5 | 10 | 11 | 13.5 | 15 |
| Seat 7 (BR) | 2 | 2 | 3 | 3 | 4 |
| Seat 8 (GWB) | 8 | 10 | 12 | 14 | 16 |
I like numbers.
The tables in part the second give us nice lower and upper bounds of the number of duals a player is expected to draft. However, upon further consideration, I think that sigh's hypergeometric calculations are a bit too optimistic. They just calculate how likely you are to pull one out of all of your captured duals. For a 2 color deck this is fine, since that is guaranteed to be a land that fixes for all of your colors. For a 3 color deck, however, this is not the case! Trilands and fetches complicate the calculations further, but let's not go there for now and try to keep it as simple as possible. In the end it's all about how many lands you need to consistently cast your spells. We can discuss all about what 'consistently' means, but falling back on Karsten's golden 90% rule, we have some idea. If you want to be able to cast a Goblin Guide or Elvish Mystic on turn one 90% of the time, you need 10 (untapped) mana sources of that color in your 40 card deck.
Now let's look at the lower bound for 5 duals per guild for a 2 color drafter (the RW drafter in seat 4). We see that they only were able to pick up a single dual land. Assuming an aggressive deck with 16 lands, if they split their lands roughly down the middle, slightly favoring red, they have a 8/7 split in basics, for 9 red sources and 8 white ones. If we reference Karsten's table... wait, let's just include that table here while crediting Frank Karsten!
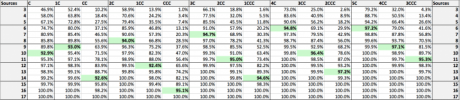
Right, if we reference this table, we can see that 9 red sources gives you 89.8% odds to be able to cast Goblin Guide on turn one. Not too shabby I would say, that's easily close enough to 90% be fine.
As an aside, note that casting a RR drop on turn two with 9 red sources has only 63.9% odds! This is one of the reasons why I try to really limit the number of CC drops in my cube (currently Counterspell is the only CC spell, and that's a reactive spell that doesn't necessarily need to be cast on turn two). I think you can only get away with CC creatures if you run a 1 to 1.5 color environment, or if you run really high numbers of fixing. Even with 8 duals per color, our RW drafter only nabbed two of them, which still doesn't bring them close to the 13 to 14 sources needed to reliably cast that Eidolon of the Great Revel on turn two consistently in their two color deck!
Back to our RW drafter with one dual. For the white cards, the odds are obviously lower, you're only running 8 white sources after all. As long as you limit yourself to XC costs for white (so, , and cards) you should be fine. This is definitely a thing cube curators should be aware off when deciding on includes! If you choose to include only 5 duals per guild (at 360, increase accordingly for larger cube sizes), make sure you have enough cards with a single pip at lower mana values to make sure your drafters can cast their cards.
Alright, time to look at a 3 color drafter. Let's take, again, the lower bound (the WBR drafter in seat 2) for 5 total duals per guild. At first blush, 7 duals (we're looking at the lower bound, so let's round down) still sounds like plenty of fixing, but let's do some calculations. Assuming a 3 color with a less than optimal fixing count chooses to run 17 lands, you're left with 10 basics. We have 2 WB, 3 BR, and 2 RW to work with, starting us off with 4 W sources, 5 B sources, and 5 R sources. If we split the 10 basics 4/3/3, we have 8 sources for every color. So, in essence, every color here is like the white color for our 2 color drafter. I think those numbers are on the edge of annoying, because every color is slightly undersupported by your mana base (while running a land more than the RW drafter as well). Note, however, that this situation will improve if you run fetches and trilands in your cube. Say two of those 7 duals are a Bloodstained Mire (replacing a BR dual) and a Savai Triome (replacing a BW dual), and suddenly you're starting off with 5 W sources, 5 B sources, and 6 R sources, before adding basic lands, giving you a mana base of roughly equal quality as the RW drafter (two colors with 9 sources, one with 8).
Cool! So 5 duals per guild does appear to be the right number then?
Now let's look at the lower bound for 5 duals per guild for a 2 color drafter (the RW drafter in seat 4). We see that they only were able to pick up a single dual land. Assuming an aggressive deck with 16 lands, if they split their lands roughly down the middle, slightly favoring red, they have a 8/7 split in basics, for 9 red sources and 8 white ones. If we reference Karsten's table... wait, let's just include that table here while crediting Frank Karsten!
Right, if we reference this table, we can see that 9 red sources gives you 89.8% odds to be able to cast Goblin Guide on turn one. Not too shabby I would say, that's easily close enough to 90% be fine.
As an aside, note that casting a RR drop on turn two with 9 red sources has only 63.9% odds! This is one of the reasons why I try to really limit the number of CC drops in my cube (currently Counterspell is the only CC spell, and that's a reactive spell that doesn't necessarily need to be cast on turn two). I think you can only get away with CC creatures if you run a 1 to 1.5 color environment, or if you run really high numbers of fixing. Even with 8 duals per color, our RW drafter only nabbed two of them, which still doesn't bring them close to the 13 to 14 sources needed to reliably cast that Eidolon of the Great Revel on turn two consistently in their two color deck!
Back to our RW drafter with one dual. For the white cards, the odds are obviously lower, you're only running 8 white sources after all. As long as you limit yourself to XC costs for white (so
, , and cards) you should be fine. This is definitely a thing cube curators should be aware off when deciding on includes! If you choose to include only 5 duals per guild (at 360, increase accordingly for larger cube sizes), make sure you have enough cards with a single pip at lower mana values to make sure your drafters can cast their cards.Alright, time to look at a 3 color drafter. Let's take, again, the lower bound (the WBR drafter in seat 2) for 5 total duals per guild. At first blush, 7 duals (we're looking at the lower bound, so let's round down) still sounds like plenty of fixing, but let's do some calculations. Assuming a 3 color with a less than optimal fixing count chooses to run 17 lands, you're left with 10 basics. We have 2 WB, 3 BR, and 2 RW to work with, starting us off with 4 W sources, 5 B sources, and 5 R sources. If we split the 10 basics 4/3/3, we have 8 sources for every color. So, in essence, every color here is like the white color for our 2 color drafter. I think those numbers are on the edge of annoying, because every color is slightly undersupported by your mana base (while running a land more than the RW drafter as well). Note, however, that this situation will improve if you run fetches and trilands in your cube. Say two of those 7 duals are a Bloodstained Mire (replacing a BR dual) and a Savai Triome (replacing a BW dual), and suddenly you're starting off with 5 W sources, 5 B sources, and 6 R sources, before adding basic lands, giving you a mana base of roughly equal quality as the RW drafter (two colors with 9 sources, one with 8).
Cool! So 5 duals per guild does appear to be the right number then?
It was nice talking about ideal situations. Isn't it great to live in a perfect world, where every drafter finds their lane before picking up off color duals, where no drafter ends up with 23 duals because they prioritize fixing over all but the greatest of bombs, and where every dual appears in the draft because we run an 8 person pod for a 360 cube? Does this apply to your cube and playgroup? Great! You are the lucky one! I think a lot of cube drafts don't include all available lands, be it because they regularly fire smaller pods, or because the cube curator chose a cube size larger than 360. Whatever the reason, I think it's good to account for these variations in dual land availability to an extent. Two potential 'solutions' spring to mind.
1. Run more than 5 duals
This one is obvious. If you run more duals, more will show up, on average, in any given draft. When we look at the table in part the third, we can see that going up to 6 duals per guild, the numbers don't dramatically increase (for those fearing 4 color good stuff piles), but that 20% extra will mean lands are noticeably more reliable to turn up.
2. Seed your boosters
This is a method I personally employ (and I'm not the only one!), and you can increase the number of lands that show up in a draft. For example, I have 9 reserved slots in my boosters (1 for each color, artifacts, and mana fixing, and 2 for gold cards) and 6 free slots. With 64 lands in the cube, 24 of them are guaranteed to show up, and the other 40 are randomly distributed with the other 194 'leftovers' over the 8 * 3 * 6 total free slots available in an 8 people pod. This gives those free slots a 40/194 chance of being a land, for another 29.7 lands on average. So, every draft will feature on average 53.7 lands, slightly over the 5 duals per guild on average.
Okay, actually, I run only 5 guilds, not 10, and I do run trilands and fetches, so my numbers are a little different in practice, but you catch my drift.
3. Nobody expects the Spanish inquisition!
See, my cube actually uses a secret way to ensure better mana bases. By supporting only 5 guilds, instead of 10, there are more lands per guild. Sure, more people will fight over each guild (2.4 on average, instead of 1.6), but there are way more duals per guild! I run 10 UB duals, for example, including two Polluted Delta. In addition, I also run four trilands that include UB as two of their colors, and four Prismatic Vistas. Then there's also 4 off color fetches that can fetch an UB dual (either one of the four UB duals, or one of the four triomes). So, a UB drafter in my cube is interested in a whopping 22 duals, rather than only 5!
4. A very fetching argument
While most cubes don't limit the number of guilds they support, the example above shows the real power of fetches. Sure, they can enable that annoying drafter that picks up every land they see, but they also increase the number of potential duals each drafter can pick up, increasing their odds of cobbling together a functioning mana base. Even if you run only one fetch per guild, and two typed duals (like Watery Grave), picking up one of those typed duals immediately opens up an additional 6 off color fetches, doubling the number of duals that fix your mana!
1. Run more than 5 duals
This one is obvious. If you run more duals, more will show up, on average, in any given draft. When we look at the table in part the third, we can see that going up to 6 duals per guild, the numbers don't dramatically increase (for those fearing 4 color good stuff piles), but that 20% extra will mean lands are noticeably more reliable to turn up.
2. Seed your boosters
This is a method I personally employ (and I'm not the only one!), and you can increase the number of lands that show up in a draft. For example, I have 9 reserved slots in my boosters (1 for each color, artifacts, and mana fixing, and 2 for gold cards) and 6 free slots. With 64 lands in the cube, 24 of them are guaranteed to show up, and the other 40 are randomly distributed with the other 194 'leftovers' over the 8 * 3 * 6 total free slots available in an 8 people pod. This gives those free slots a 40/194 chance of being a land, for another 29.7 lands on average. So, every draft will feature on average 53.7 lands, slightly over the 5 duals per guild on average.
Okay, actually, I run only 5 guilds, not 10, and I do run trilands and fetches, so my numbers are a little different in practice, but you catch my drift.
3. Nobody expects the Spanish inquisition!
See, my cube actually uses a secret way to ensure better mana bases. By supporting only 5 guilds, instead of 10, there are more lands per guild. Sure, more people will fight over each guild (2.4 on average, instead of 1.6), but there are way more duals per guild! I run 10 UB duals, for example, including two Polluted Delta. In addition, I also run four trilands that include UB as two of their colors, and four Prismatic Vistas. Then there's also 4 off color fetches that can fetch an UB dual (either one of the four UB duals, or one of the four triomes). So, a UB drafter in my cube is interested in a whopping 22 duals, rather than only 5!
4. A very fetching argument
While most cubes don't limit the number of guilds they support, the example above shows the real power of fetches. Sure, they can enable that annoying drafter that picks up every land they see, but they also increase the number of potential duals each drafter can pick up, increasing their odds of cobbling together a functioning mana base. Even if you run only one fetch per guild, and two typed duals (like Watery Grave), picking up one of those typed duals immediately opens up an additional 6 off color fetches, doubling the number of duals that fix your mana!
TLDR; Hahaha... Ha... ha... Oh, do I really have to write a synopsis?! o_O Ok then...
- 5 duals per guild at 360 seems like a good number to strive for if you have a 2 to 2.5 color environment.
- I strongly recommend going up to 6 duals per guild per 360 if you typically don't draft your entire cube (either because you run draft pods with less than 8 people, or because you run a 450+ cube, in the last case, multiply accordingly).
- Fetches are fricking amazing, run them! Running one fetch per guild more than doubles the number of potential lands a 2 color drafter can pick up from 5 to 11 once they pick up a typed dual in their colors.
- Finally, seeding your boosters can improve the mana bases of your drafters significantly.
Last edited:
6 drafted duals means you have 11 other land slots for basics. Thats where other lands in my calculations come from. I did fudge the numbers a bit for simplicity sake. You cover it in more depth in part the Third.
One correction is I did mean to write on the *draw* not on the play in my details. It was late.
D:
Evolving Wilds style fetches are also amazing for a similar reason. One of these lands flexibly accounts for any and all colors represented in any deck. Adding 5 EW variants adds 5 to every drafters relevant lands while only adding 5 land slots, and they are slightly "worse" than dual/fetch fixing so they can usually be picked up by a drafter who needs them.
Actually, I'm going to go as far as saying the first "cycle" of lands most designers should look at adding if they want to increase land count is the five "Evolving Wilds" (Ash Barrens, Evolving wilds, Terramorphic expanse, Fabled passage, Prismatic vista). That puts every 2 color drafter from 4 to 9 relevant lands in a draft, ""equivalent"" to adding 50 non-fetch duals.
Furthermore, this effect is strongest for 2 color decks, so adding these types of lands helps prevent the diminishing viability of 2C decks as laid out in my above novel. Three color decks also only get +5 lands, so aren't disproportionately helped like when adding duals, and percentage-wise get fewer new options than 2 color: +42% vs. +125% on 2 color decks
run evolving wilds. They are good for format health.
Has anyone tried Envolving Wild style fetches in the basic land box? Is this a good / bad idea?
Onderzeeboot
Ecstatic Orb
Yes (not me) and yes. Whatever lands you decide to run in your basic land box, I believe they should not diminish the desirability of the mana fixing in your main cube too much, which makes actual Evolving Wilds (or Terramorphic Expanse if you prefer that name and art) or Ash Barens the most likely candidates for the basic land box. I think Prismatic Vista is a bit too high quality to just hand out willy nilly.
For lower power I think unknown shores can work well in the BLB also. Mirrodin's core another option.